[수치해석] Linear Least-Squares Rgression(최소제곱 회귀 분석), 결정계수
1. Regression(회귀), Interpolation(보간법)
데이터 분포를 직선, 다항함수, ... 등 하나의 대표하는 함수로 표현하는 것을 regression, 회귀라고 한다.
데이터들이 상당한 크기의 오차를 포함하거나, "산재한" 경우 사용한다.

<데이터의 분포를 직선으로 회귀한 모습>
여기서, 또 하나의 개념이 등장한다
Interpolation(보간법): 각 점을 직접 통과하는 직선이나 일련의 곡선을 구하는 것을 말한다.
데이터가 매우 정확하게 알려져 있는 경우 사용한다.
Regression(회귀), interploation(보간법)의 차이:
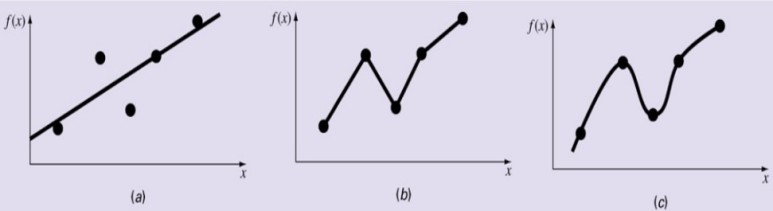
동일한 데이터에 대해 (a) 최소제곱 회귀분석 (회귀), (b) 선형보간법, (c) 곡선보간법을 적용한 예시다.
셋 다 데이터를 대표하는 방법이지만, 그림을 보면 차이를 쉽게 알 수 있을 것이다.
보간법은 점을 무조건 지나치지만, 회귀는 점을 지나지 않고 모델과 data간의 오차가 최소화되는 방향으로 업데이트되는 개념이다.
n개, 혹은 그보다 많은 데이터 대표화하기:
n개의 데이터가 존재할때, n-1차 다항 함수로 interpolation 할 수 있다.
ex) 3개의 데이터로 이차함수 interpolation -> 이차함수는 상수항까지 포함해서 미지수 3개이므로 데이터가 3개 필요하다
n개보다 더 많은 데이터가 존재할땐, n-1차 다항함수로 interpolation이 불가능하다. (미지수가 n개지만 데이터가 n보다 더 많으므로 함수가 데이터들의 점을 다 지나갈 수 없다.) -> 이럴땐 regression을 사용한다.
2. Standard derivation
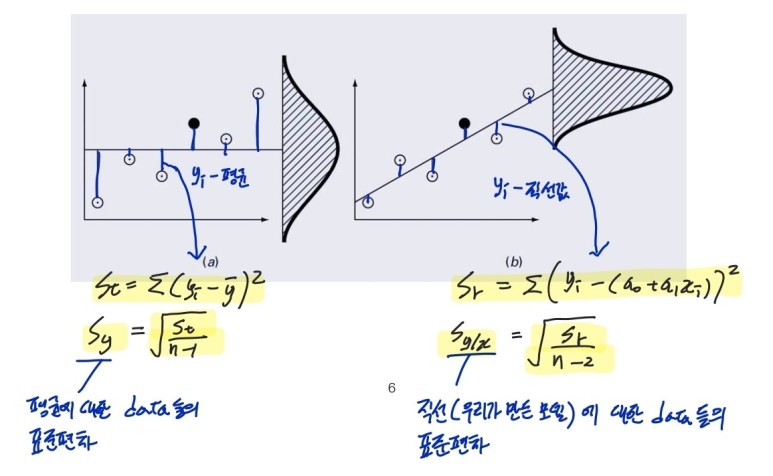
주어진 input/ output 데이터(x1, y1), (x2, y2), (x3, y3), ....를 대표할 수 있는 직선 모델을 y라고 할 때, 일차함수인 y는
로 나타낼 수 있고, 여기서 e는 모델 y와 실제 데이터 사이의 차이인 오차, residuals 이라고 한다.
식으로 표현한다면 i번째 데이터의 값 yi - 그에 따른 직선모델 y 값,
e = (yi - (a0+a1xi)) 로 둘 수 있다. (위의 식에서 이항 후 값을 대입한 형태)
그리고 평균과 데이터의 표준편차를 sy라고 표현했다면, 직선모델과 데이터의 표준편차, standard derivaton(sy/x)도 있다.
그림으로 쉽게 이해하기!
3. Coefficient of determination (결정계수)
input과 output의 상관관계를 나타낸다.
직선으로 fitting을 한 모델이 얼마나 의미가 있는지, 없는지 1에서 0 사이의 값으로 알 수 있다.
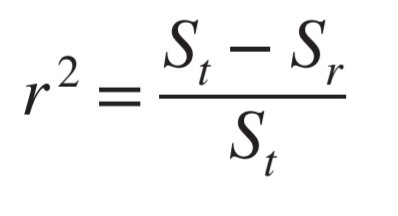
로 구할 수 있다.(St, Sr이 무엇인지는 바로 위의 그림 참고!)
좀 더 직관적으로는
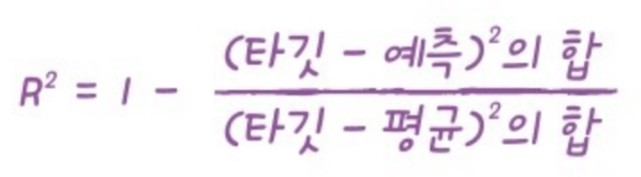
이 되겠다.(여기서 말하는 타깃은 각 데이터, 예측은 직선모델)
예시:
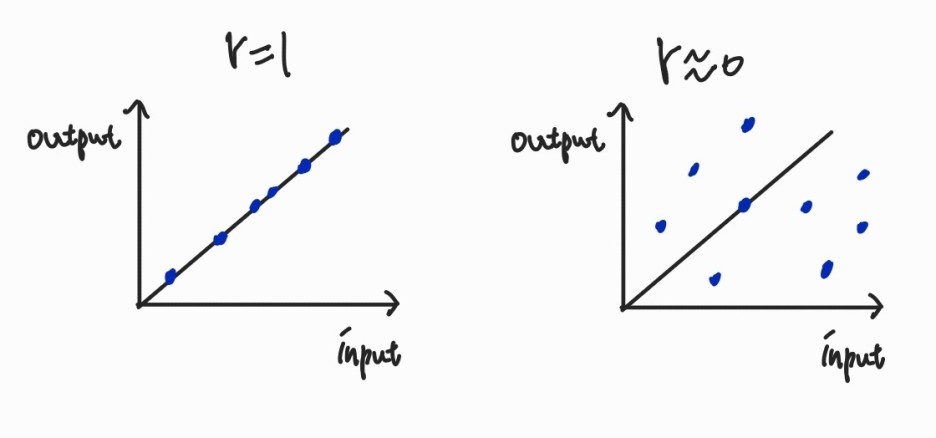
r이 1이라면 데이터가 전부 직선에 놓여있는 완전접합, r이 0이라면 직선이 데이터와 아무 상관 없는, 의미 없는 fitting임을 뜻한다.
의미만 알고 넘어가도 되는 개념이다!
4. Linear Least-Squares Rgression(최소제곱 회귀 분석)
최소제곱 회귀 분석은 이러한 직선모델 중 최적의 직선을 뽑는 방법 중 하나다.
직선 회귀 모델과 데이터간의 차이(오차)의 제곱의 합을 최소로 만드는 것을 Linear Least-Squares Rgression이라고 한다.
즉, Sr을 최소로 만든다!
머신러닝에서 주로 쓰인다.
5. Least squre solution을 구하는 방법 (행렬로 데이터가 주어졌을때 )

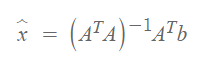
로 a0 , a1 을 구한 다음, y = a0 + a1x 형태로 나타내주면 끝!
Linear regression 뿐만 아니라 다차할 모델인 poly regression도 같은 솔루션으로 구할 수 있다.