| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 토끼와 경주
- 순서대로방문하기
- 삼성기출
- 마법의숲탐색
- 싸움땅
- 백준
- ros
- 3Dreconstruction
- PQ
- 시뮬레이션
- 왕실의기사대결
- ARM
- 나무박멸
- 코드트리빵
- BFS
- 포탑부수기
- 수영대회결승전
- 슈퍼컴퓨터클러스터
- ICER
- 소프티어
- 구현
- 조합
- 이진탐색
- Calibration
- DP
- 코드트리
- DenseDepth
- 루돌프의반란
- 마이크로프로세서
- dfs
- Today
- Total
from palette import colorful_colors
[논문리뷰] LeNet-5 + 합성곱층과 풀링층 설명, Pytorch 코드 첨부 본문
1. LeNet-5
Gradient-Based Learning Applied to Document Recognition(1988)
YANN LECUN, MEMBER, IEEE, LEON BOTTOU, YOSHUA BENGIO, AND PATRICK HAFFNER
이미지 분류를 위한 신경망, CNN 계열의 원조격 모델이다. 합성곱 신경망이라는 개념을 얀 르쿤이라는 사람이(Yann LeCun) 최초로 개발한 구조다. 수표에 쓴 손글씨 숫자를 인식하는 딥러닝 구조이며, 합성곱(Convolutional)과 다운 샘플링(sub-sampling)을 반복한 후 마지막 완전연결층에서 분류를 수행한다.
합성곱층과 풀링층의 필요성
모델 구성을 알아보기 위해 합성곱층과 풀링층이 각각 무엇인지 소개하겠다.
이미지는 픽셀 하나하나마다 딥러닝 모델에서의 특성이라고 할 수 있다. (예를 들어 물고기 분류시 무게, 폭, 길이 총 3개의 특성만 사용한다고 할때, 28x28사이즈의 이미지는 784개의 특성이 존재하는 것이다.)
모든 특성을 반영한다면 좋겠지만 처리할 수 있는 하드웨어는 한정적이다. 따라서 차원 축소가 필요하다.
또 그 많은 특성 중 주요한 특성만 추출할 수 있는 연산이 필요하다.
그래서 이러한 특성을 효율적으로 줄여 연산량을 감소시키고, 주요 특성 벡터를 추출해 학습을 효과적으로 하기 위해
합성곱층과 풀링층이 사용된다.
2. Convolutional layer(합성곱층)
합성곱층은 입력 데이터에서 특성을 추출하여 줄이는 역할을 수행한다. 이미지가 들어왔을때 이미지에 대한 특성을 감지하기 위해 커널/필터를 사용하고, 이 커널/필터는 한번에 스트라이드(보폭)라는 지정된 간격만큼 이동하며 특성을 추출하게 되는데, 이렇게 추출한 결과물이 feature map(특성맵)이다. 커널은 보통 3x3 크기로 적용되는것이 일반적이다.
다음은 3×3 크기의 커널로 5×5의 이미지 행렬에 합성곱 연산을 수행하는 과정이다.
- 첫 번째 스텝
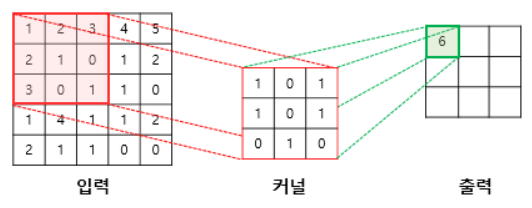
(1×1) + (2×0) + (3×1) + (2×1) + (1×0) + (0×1) + (3×0) + (0×1) + (1×0) = 6
- 두 번째 스텝
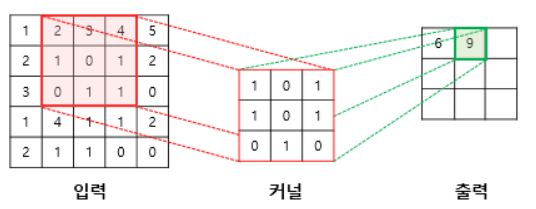
(2×1) + (3×0) + (4×1) + (1×1) + (0×0) + (1×1) + (0×0) + (1×1) + (1×0) = 9

이렇게 9번의 스텝 후 최종 특성맵이 만들어진다.
위는 그레이스케일(흑백) 이미지에 대한 합성곱층 적용이고, 컬러 이미지 합성곱은 다른 특징을 가지고 있다.
- 필터 채널이 3이다.(R, G, B)
- RGB 각각에 서로 다른 가중치로 합성곱을 적용한 후 결과를 더해준다.
필터가 2개 이상이라면 필터 각각은 특성 추출 결과의 채널이 된다.
예를 들어 28 x 28 x 3인 RGB 이미지를 4개의 필터를 이용했다면 특성맵은 26 x 26 x 4가 된다. (채널이 총 4개 만들어짐)
합성곱층 요약:
- 입력 데이터: W1 x H1 x D1 (W1: 가로, H1: 세로, D1: 채널 또는 깊이) 일때,
- 하이퍼 파라미터: K(필터 개수), F(필터 크기, 예를 들어 3x3필터면 F = 3), S(스트라이드), P(패딩, 합성곱시 여백에 추가로 덧붙이는걸 말한다)
- 출력 데이터: W2 = (W1 - F + 2P)/S + 1, H2 = (H1 - F + 2P)/S + 1, D2 = K
합성곱층 특성맵의 크기 계산 방법:
즉, 가로 세로가 같은 이미지의 합성곱층 통과 출력 데이터의 폭 크기:
(W - F +2P)/S + 1
3. sub-sampling(다운 샘플링), 또는 Pooling layer(풀링층)
합성곱층과 유사하게 특성 맵의 차원을 다운샘플링해 연산량을 감소시킨다.
예를 들어 필터 크기가 2x2라면 이미지를 1/4로 축소시킨다고 생각하면 된다.
풀링에는 두 가지 종류가 있다.
- max pooling(최대 풀링) - 대상 영역에서 최대값 추출
- avarage pooling(평균 풀링) - 대상 영역에서 평균 반환
대부분 합성곱 신경망에선 최대 풀링이 사용되는데, 평균 풀링은 각 커널 값을 평균화시켜 중요한 가중치를 갖는 값의 특성이 희미해질 수 있기 때문이다.
아래의 그림은 max pooling을 이용해 4x4 이미지를 2x2 특성맵으로 변환하는 과정이다.

합성곱층 요약:
- 입력 데이터: W1 x H1 x D1
- 하이퍼 파라미터: F(필터 크기), S(스트라이드)
- 출력 데이터: W2 = (W1 - F)/S + 1, H2 = (H1 - F)/S + 1, D2 = D1
특성맵의 크기 계산 방법:
즉, 가로 세로가 같은 이미지의 풀링층 통과 출력 데이터의 폭 크기:
합성곱층 공식에서 깊이가 변하지 않고 패딩이 없다는 점을 생각하면 된다.
(W - F +2P)/S + 1
4. Fully connected layer(완전연결층)
합성곱층과 풀링층을 거치면서 차원이 축소된 특성 맵은 최종적으로 완전연결층으로 전달된다. 이 과정에서 이미지는 3차원 벡터에서 1차원 벡터로 펼쳐지게 된다.

5. LeNet - 5 모델구성
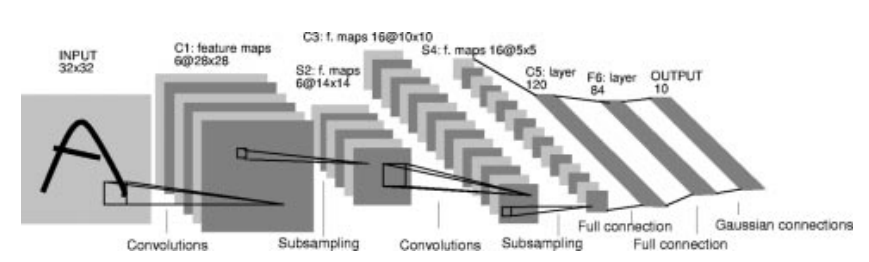
합성곱층, 풀링층, 완전연결층을 알았다면 Lenet 구조를 분석해보자.
입력 이미지는 합성곱층 → 다운샘플링(풀링) → 합성곱층 → 다운샘플링(풀링) → 합성곱층 → 완전 연결층을 통과한다.
C1: 5x5 합성곱 연산 후 28 x 28 특성맵 6개 형성
S2: 2x2 max pooling layer로 특성 맵 크기를 14 x 14로 줄인다
C3: 5x5합성곱 연산 후 10 x 10 특성맵 16개 형성
S4: 2x2 max pooling layer로 특성 맵 크기를 5 x 5로 줄인다
C5: 5x5 합성곱 연산 후 1 x 1 크기의 특성맵 120개 형성
F6: 완전연결층으로 120개의 노드를 84개에 연결
최종 출력: 10개, 따라서 10개 노드 중 제일 높은 값이 나온 것으로 이미지를 해석한다.
활성화함수는 합성곱층과 완전연결층은 ReLU, 최종 출력층은 소프트맥스를 사용한다.
6. pytorch 코드
모델 구성 부분만 코드를 작성했다. 이 코드는 인풋 크기가 3x224x224인 이미지를 사용해서 논문의 28x28 사이즈와는 다르다.
# 모델의 네트워크 클래스 정의
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.cnn1 = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=5, stride=1, padding=0) # input:(3,224,224), output: (16,220,220)
self.relu1 = nn.ReLU()
self.maxpool1 = nn.MaxPool2d(kernel_size=2) # polling output: (16,110,110)
self.cnn2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=5, stride=1, padding=0) # output:(32,106,106)
self.relu2 = nn.ReLU() # activation
self.maxpool2 = nn.MaxPool2d(kernel_size=2) # output: (32, 53, 53)
self.fc1 = nn.Linear(32*53*53, 512)
self.relu5 = nn.ReLU()
self.fc2 = nn.Linear(512, 2)
self.output = nn.Softmax(dim=1)
def forward(self, x): # forward 과정
out = self.cnn1(x)
out = self.relu1(out)
out = self.maxpool1(out)
out = self.cnn2(out)
out = self.relu2(out)
out = self.maxpool2(out)
out = out.view(out.size(0), -1) # 완전연결층으로 전달하기 위해 데이터 형태를 1차원으로 바꾼다.
out = self.fc1(out)
out = self.fc2(out)
out = self.output(out)
return out
reference: https://ieeexplore.ieee.org/abstract/document/726791
Gradient-based learning applied to document recognition
Multilayer neural networks trained with the back-propagation algorithm constitute the best example of a successful gradient based learning technique. Given an appropriate network architecture, gradient-based learning algorithms can be used to synthesize a
ieeexplore.ieee.org
(lenet5 논문)
07-01 합성곱과 풀링(Convolution and Pooling)
합성곱 신경망(Convolutional Neural Network)은 이미지 처리에 탁월한 성능을 보이는 신경망입니다. 이번 챕터에서는 합성곱 신경망에 대해서 학습합니다. …
wikidocs.net
