| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- ros
- 이진탐색
- 마법의숲탐색
- DP
- 조합
- 3Dreconstruction
- PQ
- 소프티어
- 마이크로프로세서
- ICER
- 포탑부수기
- 왕실의기사대결
- 코드트리
- 순서대로방문하기
- 나무박멸
- 삼성기출
- BFS
- 백준
- 슈퍼컴퓨터클러스터
- 싸움땅
- 토끼와 경주
- 수영대회결승전
- 루돌프의반란
- 구현
- DenseDepth
- 시뮬레이션
- Calibration
- 코드트리빵
- ARM
- dfs
- Today
- Total
from palette import colorful_colors
[수치해석] Power Method, Inverse Power Method - 원하는 Eigenvalue 찾는 방법 (with MATLAB코드) 본문
[수치해석] Power Method, Inverse Power Method - 원하는 Eigenvalue 찾는 방법 (with MATLAB코드)
colorful-palette 2023. 1. 21. 21:36<목차>
1-1. power method
1-2. power method 사용 이유
2-1. power method 방법 - 가장 큰 eigenvalue찾기
※ MATLAB에서 eigenvalue를 구하는 함수, eig()
2-2. Inverse power method 방법 - 가장 작은 eigenvalue or 내가 원하는 위치의 eigenvalue 찾기
3. power method 과제 MATLAB code
1-1. Power method
eigenvalue가 존재하는 행렬 A에서 (squre matrix), Dominant eigenvalue, 즉 가장 큰 eigenvalue(고윳값)을 찾는 알고리즘입니다.
기존 power method는 가장 큰 eigenvalue를 찾는 알고리즘이지만, 수식을 변경해서 가장 작은, 혹은 내가 원하는 위치의 eigenvalue를 구할 수도 있습니다.
1-2. 그래서, Power method 어따 써먹는데?
예를 들어

같은 시스템을 생각해 봅시다.
이 시스템에서 transient response인 x(t)는

로 나타나집니다. 즉, x(t)는 eigenvalue와 eigenvector에 의해 결정된다고 볼 수 있습니다.
따라서 만약 x(t)를 변경 혹은 분석하고 싶을 경우, 시스템에 제일 큰 영향을 줄 수 있는 성분인 가장 큰, 혹은 가장 작은 eigenvector를 구할 때 이용됩니다.
ex) 이러한 시스템의 진동 분석에 이용될 수 있습니다.


2-1. power method - 가장 큰 eigenvalue찾기
예시를 들어 설명하겠습니다.
power method를 이용해 다음 행렬의 가장 큰 eigenvalue 구하기:
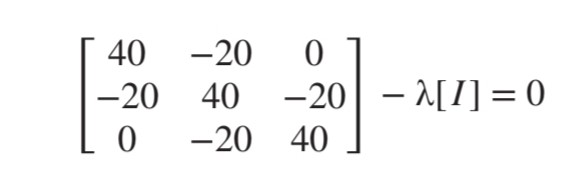
해당 행렬을 보기 쉽게 Ax = λx꼴로 정리하겠습니다.
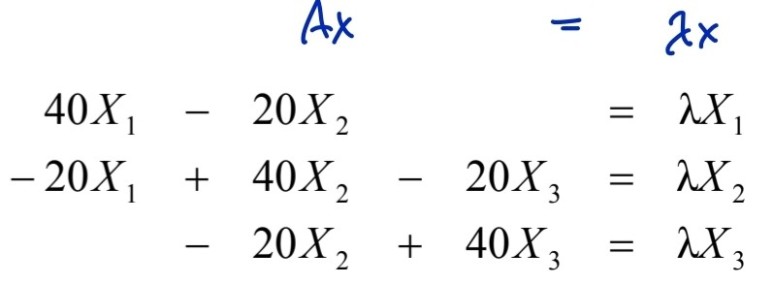
step1) 초기 x를 1벡터로 초기화하고, Ax를 계산합니다. 이후 우변쪽 x의 최댓값이 1이 되도록 정규화합니다. (λx)꼴이 되도록 만드는 것)
-> 요소 중 가장 큰 절댓값을 가지고 있는 요소를(음수 포함!) 밖으로 뺍니다
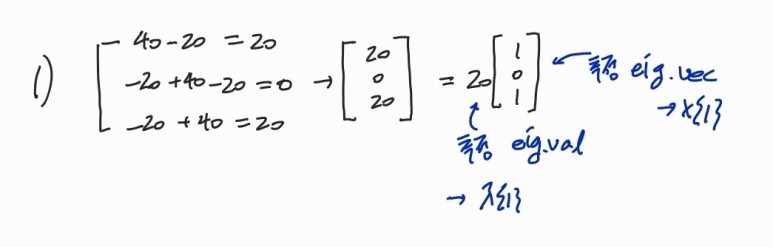
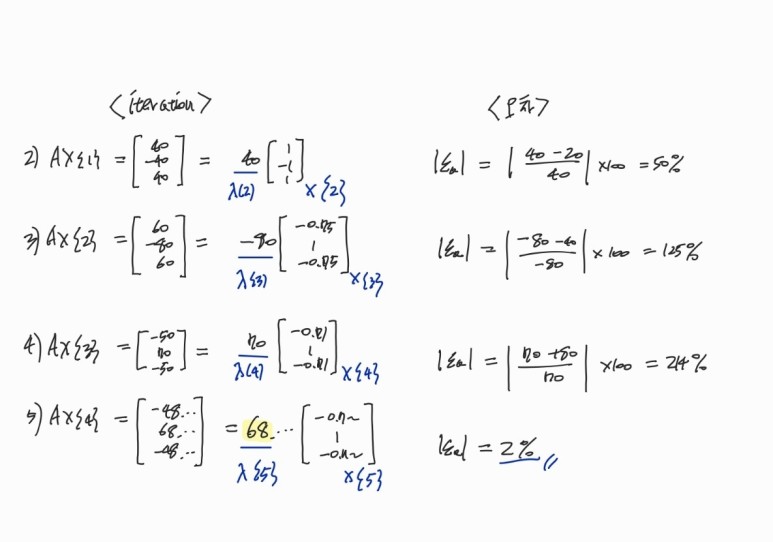
step2) step1)의 작업을 반복하여, 원하는 횟수 or 원하는 오차 미만으로 수렴할 때 까지 반복합니다.
5번의 반복 결과 행렬 A의 가장 큰 eigenvalue는 68로 나왔습니다!
※매트랩에서 eigenvalue, eigenvector 구하는 함수:
매트랩에서는 eig() 함수로 eigenvalue와 eigenvector를 바로 찾을 수 있습니다.
반환값이 한 개일때 예시:
e는 행렬의 eigenvalue들의 열백터입니다.
가장 큰 eigenvalue가 방금 전 power method로 구했던 값과 비슷하단 것을 알 수 있습니다.

반환값이 두 개일때 예시:
v는 eigenvector, lambda는 이에 해당하는 λI matrix입니다.

2-2. Inverse power method - 가장 작은 eigenvalue or 내가 원하는 위치의 eigenvalue 찾기
A의 제일 작은 eigenvalue 찾기: A의 역행렬을 power method를 이용해 제일 큰 eigenvalue를 찾고, 이를 역수시켜 얻습니다.

원하는 위치 α에 제일 가까운 eigenvalue 찾기: (A - αI)의 역행렬을 power method를 이용해 얻습니다.

과제 MATLAB code
매트랩에는 친절하게 eigenvalue를 구해주는 함수가 있지만, 직접 구현해봅시다!
학부 과제에 활용했던 문제와 코드를 첨부합니다 (변형해서 사용하면 됩니다)


교재의 power method 구하는 정의에 최대한 맞춰서 코드를 짰습니다.
problem1: 다음 행렬 A와 초기값 x0를 이용해 power method로 제일 큰 eigenvalue 구하기
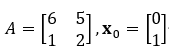
코드:
close all; clear; clc;
%%
A = [6 5;1 2];
x0 = [0; 1];
fprintf("\npower method for estimating a strictly dominant eigenvalue\n");
power_dominant(A,x0, 0.0001,6)
function power_dominant(A,evect,es,maxit)
iter=0;ea=100;eval_uk = 1; %초기화
while(1)
fprintf("iteration: %d \n", iter) % 출력을 위한 구문 %
fprintf("evect element: [%f %f] uk: %f\n", evect(1,1), evect(2,1));
eval_old = eval_uk; %save old eigenvalue value
evect=A*evect; %determine eigenvector as [A]*{x}
eval_uk=max(abs(evect)); % 제일 큰 eigenvalue
% 출력을 위한 구문 %
fprintf("Axk element: [%f %f] uk: %f\n", evect(1,1), evect(2,1),
eval_uk);
evect=evect./eval_uk; %normalize eigenvector to eigenvalue -> xk+1 =
(1/uk)Axk 계산
iter=iter+1;
if eval_uk~=0, ea = abs((eval_uk - eval_old)/eval_uk)*100; end %ea,
eval 이 0 이어서 오류가 나면 실행을 멈추도록 하는 구문
if ea<=es || iter >= maxit,break,end
end
end
결과:

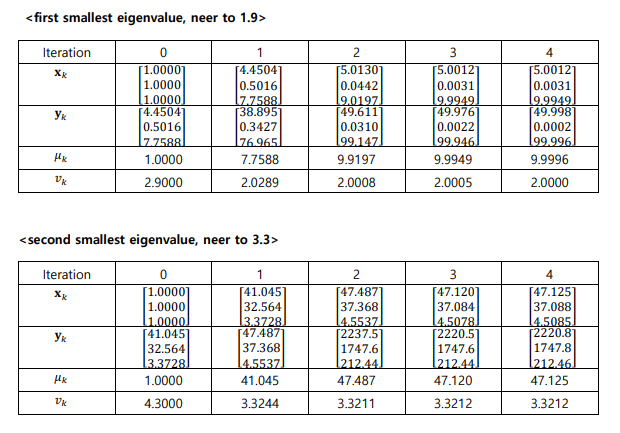
problem2: 다음 행렬 A와 초기값 x0를 이용해 inverse power method로 제일 작은 2개의 eigenvalue 구하기.
(미리 주어진 roughly estimated eigenvalues: 21, 3.3, and 1.9 일때)

close all; clear; clc;
%%
A = [10 -8 -4; -8 13 4; -4 5 4];
x0 = [1; 1; 1];
I = [1 0 0; 0 1 0;0 0 1];
alpha = 1.9; % 제일 작은 eig.val 찾을때
fprintf("\ninverse power method for estimating an eigenvalue λ with roughly
estimated eigenvalues\n");
power_inverse(A,x0, 0.0001, 5, I, alpha)
alpha = 3.3; % 두 번째 작은 eig.val 찾을때
fprintf("\ninverse power method for estimating an eigenvalue λ with roughly
estimated eigenvalues\n");
power_inverse(A,x0, 0.0001, 5, I, alpha)
function power_inverse(A,evect, es, maxit, I, alpha)
iter=0;ea=100;eval_uk= 1;%초기화
while(1)
fprintf("iteration: %d \n", iter) % 출력을 위한 구문 %
fprintf("evect element: [%f %f %f] \n", evect(1,1), evect(2,1),
evect(3,1));
eval_old = eval_uk; %save old eigenvalue value
yk = (A - alpha*I)^(-1)*evect;
eval_uk = max(abs(evect)); % 제일 큰 eigenvalue
eval_vk = alpha +(1/eval_uk);
% 출력을 위한 구문 %
fprintf("yk element: [%f %f %f] uk:%f vk:%f\n", yk(1,1), yk(2,1),
yk(3,1), eval_uk, eval_vk);
evect=yk./eval_uk; %normalize eigenvector to eigenvalue -> xk+1 =
(1/uk)Axk 계산
iter=iter+1;
%if eval_uk~=0, ea = abs((eval_uk - eval_old)/eval_uk)*100; end %ea,
eval 이 0 이어서 오류가 나면 실행을 멈추도록 하는 구문
if ea<=es || iter >= maxit,break,end
end
end결과:
'CS 학부과목 > 선형대수,수치해석' 카테고리의 다른 글
| [수치해석] Linear Least-Squares Rgression(최소제곱 회귀 분석), 결정계수 (0) | 2023.01.21 |
|---|---|
| [수치해석] 데이터 분석에 필요한 기본 통계 개념(with MATLAB) (2) | 2023.01.21 |


