| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- ros
- 삼성기출
- Calibration
- ISER
- 슈퍼컴퓨터클러스터
- dfs
- 루돌프의반란
- 코드트리
- 코드트리빵
- 구현
- 마법의숲탐색
- 시뮬레이션
- BFS
- ARM
- 나무박멸
- 3Dreconstruction
- 소프티어
- 조합
- 싸움땅
- 수영대회결승전
- DenseDepth
- 마이크로프로세서
- 순서대로방문하기
- 포탑부수기
- 이진탐색
- ICER
- DP
- 토끼와 경주
- 백준
- 왕실의기사대결
- Today
- Total
from palette import colorful_colors
[수치해석] 데이터 분석에 필요한 기본 통계 개념(with MATLAB) 본문
대푯값 - 산술평균, 중앙값, 최빈값
대푯값: 어떤 데이터를 대표하는 값
Arithmetic mean(산술평균): 모든 요소를 합하고 요소의 개수로 나눈 값 (우리가 알고 있는 일반적인 평균)

Median (중앙값): 데이터 요소 중 정확히 중앙에 있는 값.
Mode(최빈값): 데이터 그룹에서 가장 빈번하게 일어난 값.
예시: A반 60명이 수치해석 시험을 쳤을때, 44점을 받은 학생이 가장 많았고, 평균점수는 50점이었다.
-> 산술평균: 50/ 중앙값: 30등 학생의 점수/ 최빈값: 44
표준편차, 분산, 분산계수 - 데이터 집합의 분산 정도를 나타내는 값
Variance(분산): 데이터가 얼마나 퍼져있는지/ 모여있는지 알 수 있는 정도다. 분산이 크면 데이터들이 퍼져있다는 뜻이고, 작다면 데이터들이 평균 근처에 모여있다는 뜻이다. 각 요소 편차들 제곱의 평균으로 구한다. 요소 제곱 그룹의 평균 - 평균의 제곱으로도 구할 수 있다.
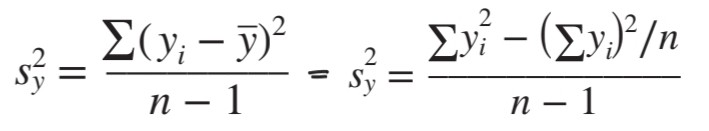
Standard deviation(표준편차): “각 데이터 요소들의 평균에서 떨어져 있는 정도” 인 편차들의 평균이라고 할 수 있다.
분산에 루트를 씌워 구할 수 있다.
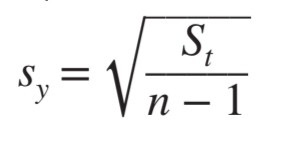
이때 St는 편차 제곱들의 합,

이다.
잠깐! 고등학교때와 다르게 왜 n이 아니라 n-1인가요?
표준편차, sy는 데이터의 '퍼져있는 정도'를 나타내는 값이므로,
포인트 하나만 있는건 의미가 없기 때문에 계산에서 제외하기 위해 n-1로 나눠준다.
-> 응용: 데이터들을 직선으로 나타낼 경우 포인트 2개만 있는 것은 의미가 없으므로, 직선에 대한 표준편차 sy/x에선 n-2로 나눠준다.
Coefficient of variation(분산계수): 분포에 대해 정규화된 척도를 말한다. 즉, 데이터 그룹의 scaile에 대한 요소를 제거한 값이다.
ex) A반의 키, 몸무게의 분포를 비교할때, 키는 m, 몸무게는 kg단위이기 때문에 키와 몸무게 두 데이터의 분산 정도를 서로 비교할 수 없다. -> 분산계수를 이용한다.
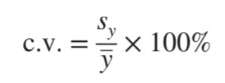
MATLAB 통계 함수 문제 예시

예시 문제를 통해 설명하겠습니다.
<답안 코드>
close all; clear; clc;
%%
% 매트랩에서 평균, 표준편차, ... 구하기
x = [0.90, 1.42, 1.30, 1.55, 1.63, 1.32, 1.35, 1.47, 1.95, 1.66, 1.96, 1.47, 1.92, 1.35, 1.05, 1.85, 1.74, 1.65, 1.78, 1.71, 2.29, 1.82, 2.06, 2.14, 1.27];
% (a) mean (평균)
fprintf("(a) mean, 평균: %10f \n", mean(x))
fprintf("(b) median, 중앙값: %10f\n", median(x))
fprintf("(c) mode, 최빈값: %10f \n", mode(x))
fprintf("(d) range, 범위(max-min): %10f \n", max(x)-min(x))
fprintf("(e) standard deviatioin, 표준편차: %10f \n", std(x))
fprintf("(f), variance, 분산: %10f \n", var(x))
fprintf("(g) coefficient of variation, 분산계수: %10f3%% \n", std(x)/mean(x)*100)'CS 학부과목 > 선형대수,수치해석' 카테고리의 다른 글
| [수치해석] Linear Least-Squares Rgression(최소제곱 회귀 분석), 결정계수 (0) | 2023.01.21 |
|---|---|
| [수치해석] Power Method, Inverse Power Method - 원하는 Eigenvalue 찾는 방법 (with MATLAB코드) (0) | 2023.01.21 |


