| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 구현
- 삼성기출
- 마이크로프로세서
- 싸움땅
- 백준
- 루돌프의반란
- 포탑부수기
- ros
- ICER
- 왕실의기사대결
- 코드트리
- 마법의숲탐색
- 수영대회결승전
- PQ
- DP
- 토끼와 경주
- dfs
- 코드트리빵
- DenseDepth
- Calibration
- 3Dreconstruction
- ARM
- 순서대로방문하기
- 나무박멸
- 소프티어
- 슈퍼컴퓨터클러스터
- 조합
- BFS
- 시뮬레이션
- 이진탐색
- Today
- Total
from palette import colorful_colors
[Computer Vision] Calibration이란?, Intrinsic parameter, extrinsic parameter 본문
[Computer Vision] Calibration이란?, Intrinsic parameter, extrinsic parameter
colorful-palette 2023. 4. 18. 21:44Computer vision에서 calibration은 카메라나 센서와 같은 장치의 내부 파라미터와 외부 파라미터를 조정하는 과정을 말합니다. 이 과정을 위해선 실제 세상의 3D 좌표계에서 픽셀의 좌표계까지 변환이 먼저 필요합니다. 이러한 변환과정과 내부 파라미터(Intrinsic parameter를 먼저 소개하겠습니다.
1. 물체점 → 영상점 → 픽셀점 까지 이동과정
실제 세상을 카메라로 담는 과정에서 실제 세상의 3D 좌표가 픽셀의 2D 좌표로 이동하게 된다.
먼저 실제 세상(물체점), 영상점(ccd 이미지 센서에 맺히는 점), 픽셀점(이미지 픽셀의 점)을 각각 다음처럼 수식으로 정의한다.

이렇게 정의한 각 3 점의 벡터를, 후에 있을 행렬 계산 편의를 위해
homogenous로 바꿔주어 차원을 더해준다 (밑에 차원 1을 더해준다)

1-1. 물체점 → 영상점

3D인 물체점 X에서 2D인 영상점x로 옮기는 과정이다.
실제 세상에 위치한 점 P(물체점)를 ccd 이미지 센서에 가져오는 과정은 위 그림과 같다.
ccd 센서는 실제로는 카메라 원점 뒤에 있어서 x = -fX/Z가 되어야 하지만 수학적 계산 편의를 위해 ccd와 물체점 모두 같은 방향에 있다고 생각하면 식이 x = fX/Z가 된다.
ccd의 y 좌표도 마찬가지로 y = fY/Z가 된다.
이를 행렬로 나타내면 아래와 같다.
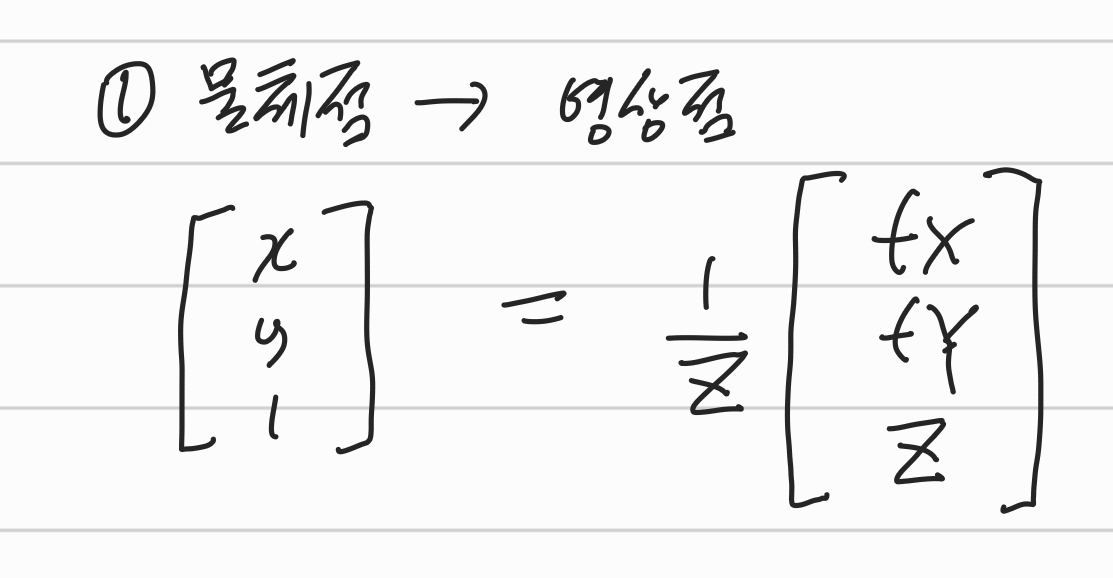
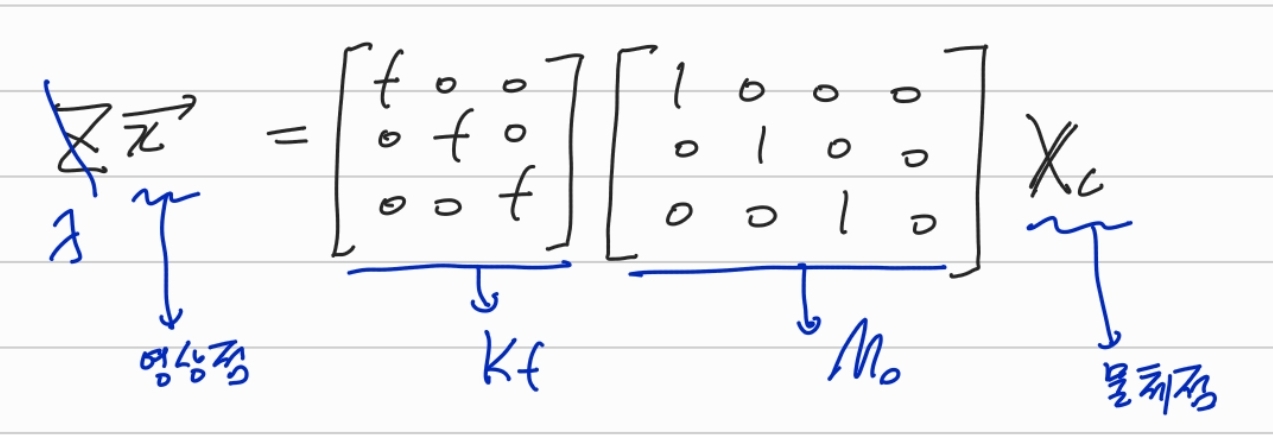
f에 관한 행렬을 따로 Kf, 이를 물체점[X Y Z 1]과 곱해주기 위한 행렬을 Mo(identity matrix다)라고 둔다.
여기서 Z는 카메라 원점에서 물체점까지의 거리이고, 실제 촬영 당시엔 모르는 값이라고 가정하고 λ로 둔다.
1-2.영상점 → 픽셀점

2D인 영상점 x에서 2D인 픽셀점x'로 옮기는 과정이다.
이때 이미지 픽셀에 맞게 스케일을 바꿔주고,
(예시: 이미지 한 픽셀이 5μm라면 1mm/5μm = 200, 스케일값은 200이 된다.)
ccd 좌표계에서 이미지 픽셀 좌표계로 이동하기 위해 (중앙에서 좌측 상단으로)
이미지의 중심 좌표인(Ox, Oy)만큼 좌표이동을 해준다.
이 변환과정을 하나의 Kf라는 행렬로 표시하는것이 위에서 점들을 homogeneous 좌표계로 변형한 이유다.
1-3. 물체점 → 영상점 → 픽셀점, Intrinsic parameter
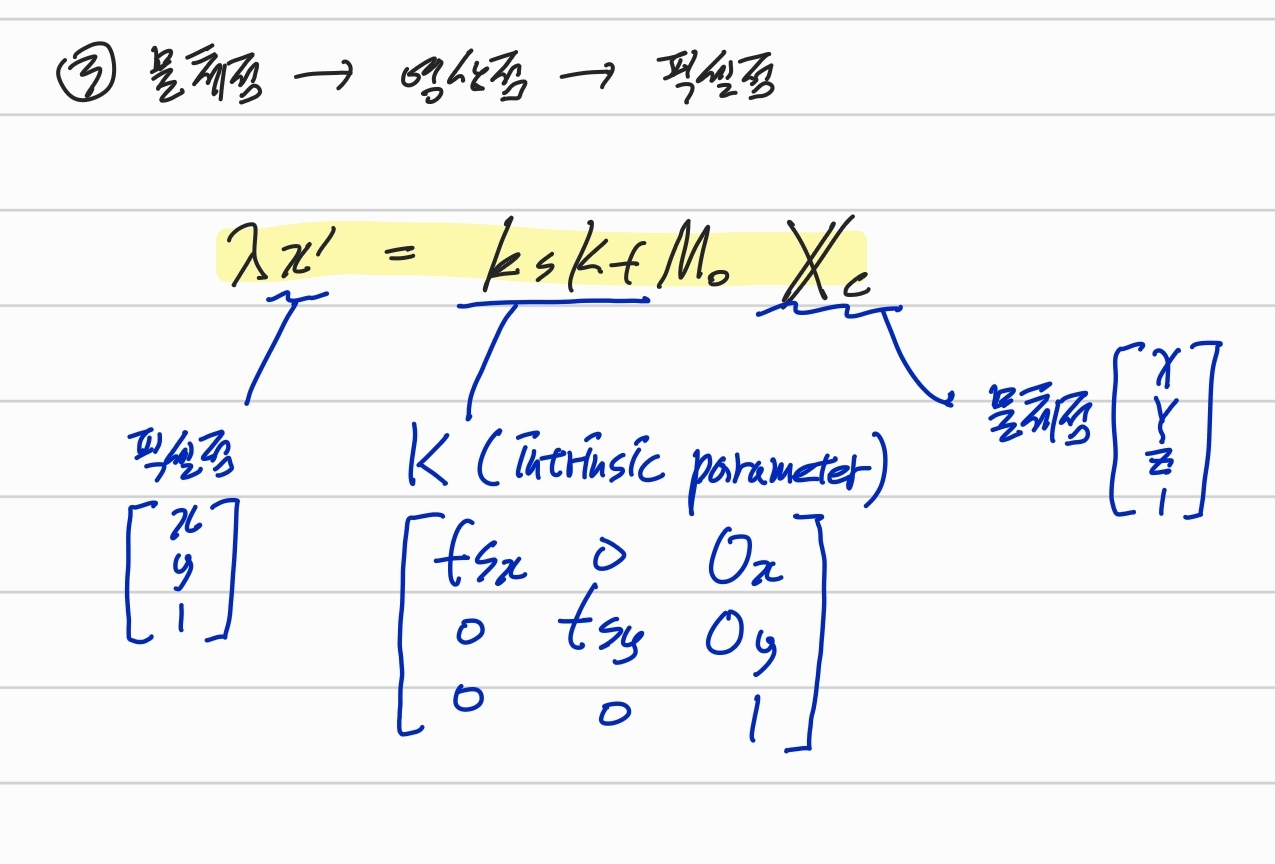
이제 최종적으로 물체점에서 픽셀점으로 변환을 해보자. 1-1, 1-2에서 설명한 두 식을 합치면 위와 같이 쓸 수 있다.
이때 물체점에서 픽셀점으로 이동할때 행렬 Ks, Kf를 합쳐서 K라고 쓸 수 있고, 이때의 K를 intrinsic parameter, 내부 파라미터라고 한다.
즉 내부 파라미터는 물체점과 픽셀점과의 관계를 나타내주는 행렬이며, 렌즈와 이미지 센서의 특성을 나타낸다고 볼 수 있다.
2. world 좌표계 → camera 좌표계의 픽셀점으로 변환, Extrinsic parameter
위에서 구한 영상점과 픽셀점간의 변환은 하나의 카메라 좌표계에서는 완벽하겠지만, 우리는 카메라 좌표계에서 살고 있지 않다. 우리는 월드 좌표계에서 살고 있다!
가령, 실제 세상의 (10, 0, 0)에 있는 카메라와 (0, 10, 0)에 있는 카메라에서 찍은 픽셀점은 분명 다를 것이다.
이를 해결하기위해 외부 파라미터가 필요한데, 아래의 과정에서 살펴보겠다.

우선 위의 1번에서 사용했던 물체점과 픽셀점간의 관계식을 가져온다.
이때 유의할점은 물체점이 카메라 좌표계에서 표시된 점임을 기억하자.

실제 좌표계에서 카메라의 좌표계로 변환할려면 rotation과 translation이 필요한데, 위에서 점들을 homogeneous로 표현했으므로 이를 한꺼번에 Me라고 표현한다.
이때 Me를 외부파라미터라고 한다. 즉 외부파라미터는 세상과 카메라의 관계를 표현해주는 파라미터다.
K와 Me를 합친 행렬을 M(ppm: perspective projection matrix)라고 하는데, 내부 파라미터와 외부 파라미터를 한번에 구할 수 있는 3x4행렬이다. 보통 체크보드를 이용해 PPM의 요소들을 구해 K와 M을 구한다.
이러한 파라미터들을 이용해 사진의 굴곡 현상도 해결할 수 있다.
더 자세한 내용은 아래 링크 참조
https://colorful-palette.tistory.com/45
[프로젝트] Checkboard Image calibration 미니 프로젝트 (with python코드)
https://github.com/woodong11/Checkboard_Calibration GitHub - woodong11/Checkboard_Calibration: 폴더 안에 들어있는 체크보드 이미지들을 이용해 python으로 calib 폴더 안에 들어있는 체크보드 이미지들을 이용해 python으
colorful-palette.tistory.com
3x 4 행렬인 PPM의 요소들을 구하는 방법은 아래와 같다.

'AI > Computer Vision' 카테고리의 다른 글
| [Computer Vision] SGBM을 이용한 Disparity Map 구하기와 meshlab을 이용한 3D reconstruction (0) | 2023.06.22 |
|---|---|
| [Computer Vision] Homography를 이용한 파노라마 만들기(python 코드 첨부) (0) | 2023.05.17 |
| [Computer Vision] opencv를 이용해 templete matching 구현하기 (0) | 2023.05.06 |
| [Computer Vision] Aperture(조리개), DoF(심도) (0) | 2023.03.20 |
| [Computer Vision] SLR, Pinhole(핀홀 카메라), Focal length(초점거리), 렌즈공식 (0) | 2023.03.20 |




